Linear Regression with Elixir and Nx
Learn how you can predict data using Linear Regression with Elixir
Table of contents
- The goal - ML Linear Regression model
- Linear Regression - How to solve it?
- Vectorized Linear Regression
- Gradient Descent - finding optimal weights
- Linear Regression in Elixir in 4 Steps
- 1. Load and prepare the data
- 2. Create ML Linear Regression model in Elixir
- 3. Test the model
- 4. Use The Model And Make Predictions!
- Linear Regression With Elixir - Conclusions
In the previous article, I made an intro to Machine Learning in the Elixir world. This time I'll show you how to actually do some real work! We'll analyze car data and try to predict the Miles Per Galon factor (label) based on related features like horsepower, engine displacement, and a few others. We'll use a Linear Regression technique for this purpose.
This post describes the whole process step-by-step of creating an ML model, testing it, and making some predictions. I'll use many useful techniques such as preparing the data, explaining Gradient Descent, writing a test, etc.
Would "a stupid straight line" be helpful in some serious Machine Learning stuff? Let's figure this out!
The goal - ML Linear Regression model
Our goal will be to analyze the CSV file with car data and try to predict the car's efficiency expressed as Miles Per Galon (MPG) based on some features using Linear Regression.
You can download the file from here. It contains almost 400 examples. Let's take a look at the data we have.
| passedemissions | mpg | cylinders | displacement | horsepower | weight | acceleration | modelyear | carname |
| FALSE | 18 | 8 | 307 | 130 | 1.752 | 12 | 70 | chevrolet chevelle malibu |
| TRUE | 22 | 4 | 140 | 72 | 1.204 | 19 | 71 | chevrolet vega (sw) |
| FALSE | 18 | 6 | 225 | 105 | 1.8065 | 16.5 | 74 | plymouth satellite sebring |
The second column contains our label - we'd like to predict MPG based on the other factors. But... what may be useful for it? Can we use more than one feature for the Linear Regression?
Linear Regression - How to solve it?
Let's start with the Linear Function formula.
$$y = wx + b$$
y is the value we'd like to predict based on x feature, which is multiplied by w (weight) and increased/decreased by b (bias). If we consider taking horsepower as the only feature, we can show it in the friendlier form.
$$MPG = w \times horsepower + b$$
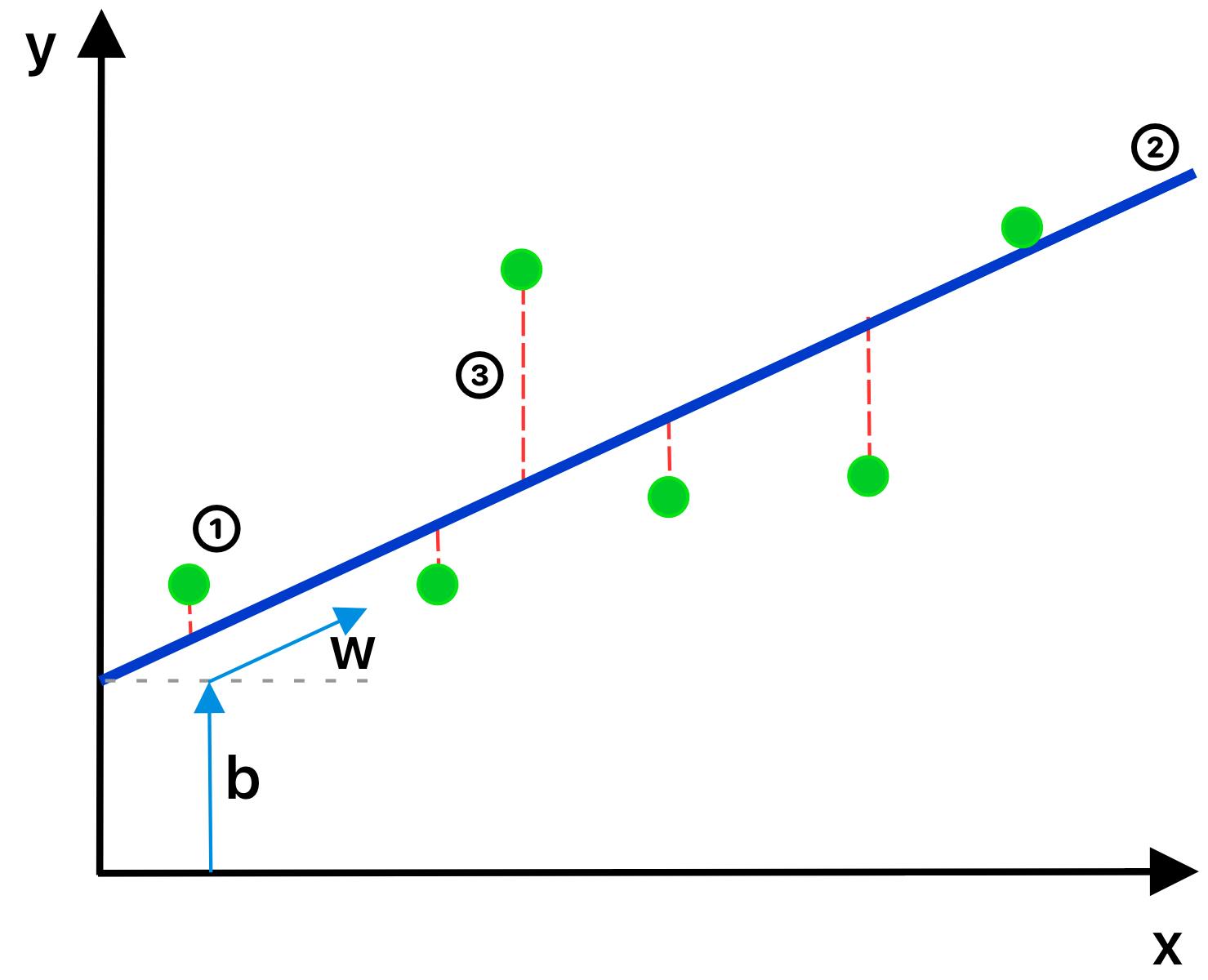
Our ultimate goal is to calculate somehow w and b, so we got the smaller possible error for the prediction. It's easier to digest it by looking at the graph.
For all data points we have ①, we'd like to determine the slope (a) and offset (b) of the prediction line ②, so we got possibly as short red dash lines ③ as possible.
Mean Squared Error - Cost Function
If we get the red lines ③ (Residual Errors) then we can calculate the overall error called Mean Squared Error (MSE) using the following formula.
$$MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i' - y_i)^2$$
Where y' is the actual value (green points like ①), and y is the prediction (line ②).
MSE lies in the range from 0 going up to some big values. "Sky is the limit" - but in this case, we're heading in the other direction - down to 0. Zero means a perfect solution! But in practice, it's unreachable. The rule of thumb: the lower the MSE, the better.
Learning = Minimizing Cost Function
Learning the ML model is about iteration through all x examples to find w and b parameters for which the cost function result is as smallest as possible. There are different optimal cost functions for different algorithms. MSE is the optimal choice for linear regression, in the Gradient Descent section you'll why.
So, we have the data... A functional programmer's intuition says "I see! We can iterate through allx-y'pairs using a reducer, do the math, and accumulate the result!". Yes! That's valid, but... Let's not do this. Not in the ML world. Let's make use of our fancy tensors!
Vectorized Linear Regression
Instead of iterating through each x and doing n calculations in the result, we'll take the vectorized approach. To make this work, we need to put all the data into tensors (particularly matrices) and do the math in just one shot!
The vectorized version of linear regression looks like this:
$$Y = \begin{bmatrix} 1 & x_1\\ 1 & x_2\\ \vdots & \vdots\\ 1 & x_n \end{bmatrix} \dot{} \begin{bmatrix} b\\ w\\ \end{bmatrix} = \begin{bmatrix} b + wx_1\\ b + wx_2\\ \vdots \\ b+ wx_n \end{bmatrix}$$
Magic or math - doesn't matter how you call it 😉. It's matrix multiplication. The first matrix contains all x values in one column and 1-s in the other. The purpose of the "1-s" column is to get b in the result. As you can see, for x1 you get wx1 + b which is exactly what we want.
For almost 400 records we have in our car models CSV file when w and b are known, we can get all y values (MPG) by doing calculations once. Now you can feel the power of proper machine learning!
Gradient Descent - finding optimal weights
Gradient descent is one of the most common techniques for learning ML models. Let's show it on the graph, so it's easier to analyze what's going on.
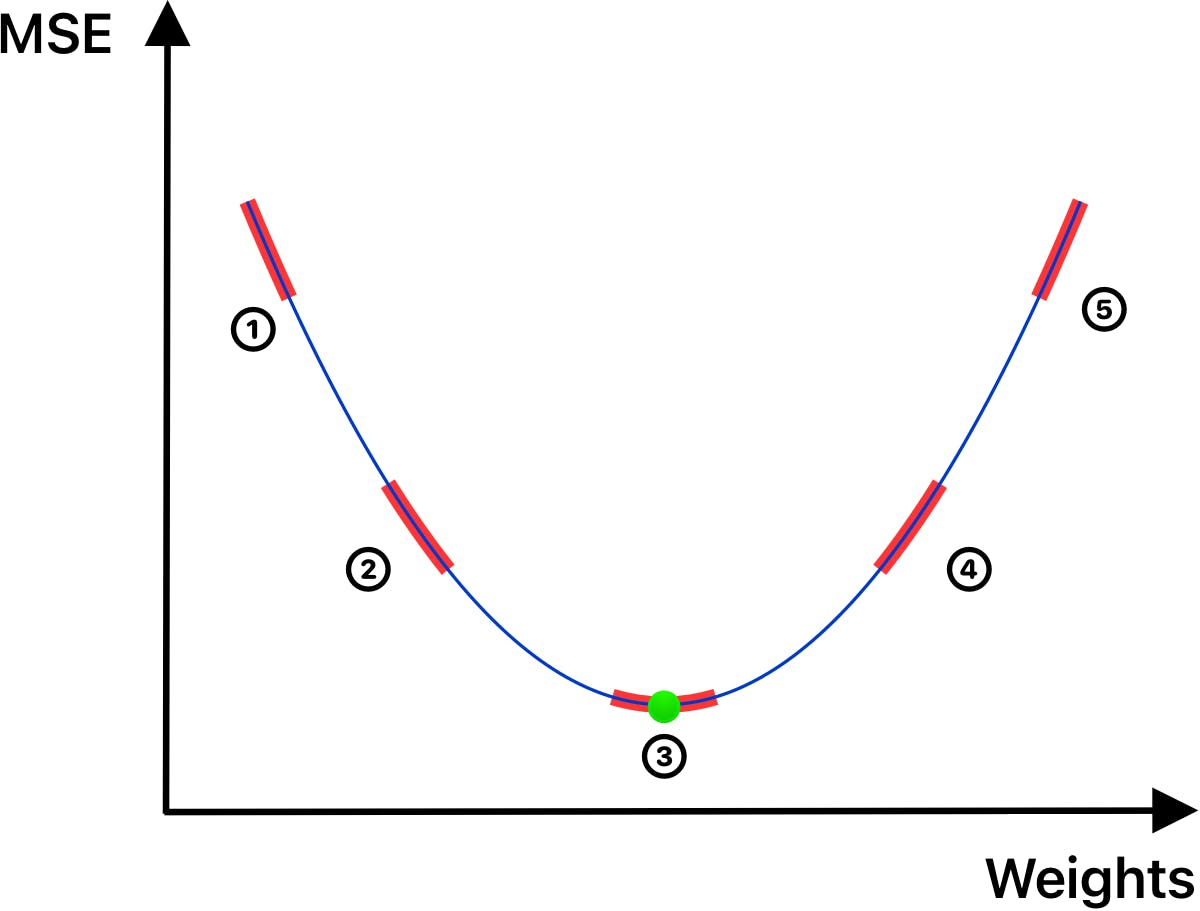
The ultimate goal is to determine weights (w and b for linear regression), so the cost function, MSE, is as close as possible to the optimal value ③. To make any progress, it needs to calculate MSE ① for some weights. MSE is an arbitrary value and in isolation, it means almost nothing. That's why gradient descent is based on slopes (red lines) rather than on the values themself.
Let's analyze some interesting parts of the graph:
① - The slope is going down hard, which means we're far from the optimal solution, but heading in the right direction
② - Now it's still going down, but more gently - we're getting closer...
③ - Optimal solution - MSE is as small as it could be, weights are optimal ✅
④ - The slope is gently rising, so we're quite close, but we overshoot with the current weights, which means that the next step of the change should be in the other direction (if weights have been increased, then should be decreased or the other way around)
⑤ - Similar as above, but worse 🙂
Remember the MSE formula?
$$MSE = \frac{1}{n} \sum_{i=1}^{n} (y'_i - y_i)^2$$
We can determine the slope by calculating the derivatives for a and b.:
$$\frac{d(MSE)}{da}= -\frac{2}{n} \sum_{i=1}^{n} x_i(y'_i - y_i)$$
$$\frac{d(MSE)}{db}= -\frac{2}{n} \sum_{i=1}^{n} (y'_i - y_i)$$
The formulas look a bit unappealing, but they make sense when described verbally: Forbtake the sum of all differences between actual and expected results. For wdo the same but additionally, multiply the differences byx. Multiply both results by -2 and divide by the numbers of all examples.
As you can guess, we can calculate derivates for all weights at once using a vectorized formula.
$$D_{MSE} = -\frac{2}{n}(F^T \cdot D)$$
Where FT is a transposed features matrix and D is the differences (y'i - yi) matrix.
An extended, generic version of the formula above looks like this:
$$D_{MSE} = - \frac{2}{n} (\begin{bmatrix} 1 & 1 & \cdots & 1 \\ x_1 & x_2 & \cdots & x_n\\ \end{bmatrix} \dot{} \begin{bmatrix} y'_1-y_1\\ y'_2-y_2\\ \vdots\\ y'_n - y_n \end{bmatrix} ) = - \frac{2}{n} \begin{bmatrix} (y'_1-y_1) + (y'_2-y_2) \cdots + (y'_n-y_n)\\ x_1(y'_1-y_1) + x_2(y'_2-y_2) \cdots + x_n(y'_n-y_n)\\ \end{bmatrix}$$
Multiple Linear Regression
We still haven't answered a pretty big question: Can we use multiple features, so besides just horsepower it also involves other data like cylinders or displacement? Yes, we can! 🙌
The standard, one-feature linear regression we discussed is called univariate. A version with multiple features is a multiple linear regression (sometimes also called multivariate, but it seems to be something else) and takes the following form.
$$y = w_1x_1 + w_2x_2 + \dotso + w_nx_n + b$$
Or in our particular case for horsepower, cylinders, and displacement.
$$y = w_1 \times horsepower + w_2 \times cylinders + w_3 \times displacement + b$$
More features equals more data. Let's take a look at how we can handle multivariate linear regression using tensors.
$$Y = \begin{bmatrix} 1 & h_1 & c_1 & d_1\\ 1 & h_2 & c_2 & d_2\\ \vdots & \vdots & \vdots & \vdots\\ 1 & h_n & c_n & d_n \end{bmatrix} \dot{} \begin{bmatrix} b\\ w_h\\ w_c\\ w_d\\ \end{bmatrix} = \begin{bmatrix} b + w_hh_1 + w_cc_1 + w_dd_1\\ b + w_hh_2 + w_cc_2 + w_dd_2\\ \vdots \\ b + w_hh_n + w_cc_n + w_dd_n \end{bmatrix}$$
I renamed x to the first character of the particular feature so it's easier to read. As you can see, handling two additional features requires adding two additional columns with values and two weights. Simple as that!👌
Linear Regression in Elixir in 4 Steps
Now it's time for the actual Elixir code! The approach I took is a "raw"/hard way, meaning everything is written from scratch. I think I'd rather use Scholar in prod, but implementing everything is way more instructive... and interesting 😉
1. Load and prepare the data
First of all, we need to decide what data may be meaningful. Certainly, we need data from the mpg column for training since it's the label in our case.
Select features
In terms of features, it's totally arbitrary what data you'll decide to use. So let's sharpen our instinct and try to answer the question: What data may affect how many miles the car can drive on one gallon?
I'm going to write more about how to meaningfully choose features. For now, let's start with the engine displacement, which seems to be appropriate. We'll see!
Load the data from CSV
Parsing CSV and retrieving data from it is fairly simple. I wrote a simple function with a hardcoded path to the file... Yes, it could be prettier and more generic, but I'll stick with simpler code so everything is clear.
defmodule LinearRegression do
alias NimbleCSV.RFC4180, as: CSV
def load_data(data_path) do
data_path
|> File.stream!()
|> CSV.parse_stream()
|> Stream.map(fn row ->
[
passedemissions,
mpg,
cylinders,
displacement,
horsepower,
weight,
acceleration,
modelyear,
_carname
] = row
{[
parse_boolean(passedemissions),
parse_int(cylinders),
parse_int(horsepower),
parse_float(displacement),
parse_float(weight),
parse_float(acceleration),
parse_int(modelyear)
], [parse_float(mpg)]}
end)
|> Enum.to_list()
end
def parse_boolean("TRUE"), do: 1
def parse_boolean("FALSE"), do: 0
defp parse_float(string_float) do
string_float |> Float.parse() |> elem(0)
end
defp parse_int(string_int) do
string_int |> String.to_integer()
end
end
load_data/1 takes a path to the file as an argument. The function loads the CSV file, and parses values to appropriate types. All values could be parsed to floats since Nx tensors use one data type for all values.
Now we'll load the data and split it into two sets: train and test.
data = LinearRegression.load_data(data_path)
{train_data, test_data} =
data
|> Enum.shuffle()
|> Enum.split(data |> length() |> Kernel.*(0.8) |> ceil())
train_count = length(train_data)
test_count = length(test_data)
x =
Enum.map(train_data, &elem(&1, 0))
|> Nx.tensor()
# take only displacement column
|> Nx.slice([0, 2], [train_count, 1])
y = Enum.map(train_data, &elem(&1, 1)) |> Nx.tensor()
x_test =
Enum.map(test_data, &elem(&1, 0))
|> Nx.tensor()
# take only displacement column
|> Nx.slice([0, 2], [test_count, 1])
y_test = Enum.map(test_data, &elem(&1, 1)) |> Nx.tensor()
It loads the data, shuffles, and splits it into 80%-20% sets. Splitting the data should be intuitive - we need some to train the model and next to test it. But why bother with shuffling? Shuffling data helps countereffect the data bias.
In this example, the data seems to be ordered by the time of releasing the particular model. This introduces bias because if you quickly peek at MPG, it's relatively lower for older models, and higher for the more recent ones. To make sure we have pretty much similar data for training and test sets, you always should shuffle it before splitting.
Prepare features for vectorized calculations
Do you remember the formula we're going to use to calculate Y?
$$Y = \begin{bmatrix} 1 & x_1\\ 1 & x_2\\ \vdots & \vdots\\ 1 & x_n \end{bmatrix} \dot{} \begin{bmatrix} b\\ w\\ \end{bmatrix} = \begin{bmatrix} b + wx_1\\ b + wx_2\\ \vdots \\ b+ wx_n \end{bmatrix}$$
We need to prepend X with the column of 1s.
defmodule LinearRegression do
import Nx.Defn
defn prepend_with_1s(x) do
ones = Nx.broadcast(1, {elem(Nx.shape(x), 0), 1})
Nx.concatenate([ones, x], axis: 1)
end
end
Notice it is defn, not ordinary def function. It's a special form of Nx function optimized for tensor calculations. TBH I'm not sure if it's the most elegant way of achieving it but... it works for me 😉.
2. Create ML Linear Regression model in Elixir
Now let's take a look at the "meat" - linear regression implementation in Elixir.
Handle state with struct
Unlike Python, Elixir is a functional programming language and doesn't support the idea of classes and instances. How to handle the state?
I could use plain map, but I'm not a big fan of using unmeaningful "bags" for data. I'm going to use a similar, simple but more powerful data type - struct.
defmodule Model do
defstruct weights: nil,
alpha: 0.1,
mse_history: [],
epochs: 100,
epoch: 0
@type t :: %__MODULE__{
weights: Nx.t() | nil,
alpha: float(),
mse_history: [float()],
epochs: integer(),
epochs: integer()
}
end
The most important part of the Model structure is weights attribute, finding optimal weights is the ultimate goal. alpha is the learning rate, mse_history is a list of MSE values, for visualization purposes. epochs determines how many training iterations we want to run and epoch is the number of the current iteration.
The training function
defmodule LinearRegression do
def train(%Model{epochs: epochs, epoch: epoch} = model, x, y) when epoch <= epochs - 1 do
{x, model} =
if epoch == 0 do
new_x = prepend_with_1s(x)
{new_x, %{model | weights: Nx.broadcast(0, {elem(new_x.shape, 1), 1})}}
else
{x, model}
end
w = gradient_descent(x, model.weights, y, model.alpha)
mse = mse(x, w, y) |> Nx.to_number()
IO.puts("Epoch: #{model.epoch}, MSE: #{mse}, weights: #{w |> Nx.to_flat_list() |> inspect}\n")
model =
model
|> Map.put(:weights, w)
|> Map.update(:epoch, 1, &(&1 + 1))
|> Map.update(:mse_history, [], &[mse | &1])
train(model, x, y)
end
def train(%Model{} = model, _x, _y) do
model
|> Map.update(:mse_history, [], &Enum.reverse/1)
end
end
train function prepends x with 1-s in the first iteration and sets weights to a tensor of 0-s. The ordinary iteration contains the calculation of new weights using gradient descent and MSE. Then it updates the Model struct and recursively calls itself with the new model.
Finally, when it runs out of iterations, it reverses mse_history to be in the right order and returns model.
defmodule LinearRegression do
defn gradient_descent(x, w, y, alpha) do
y_pred = Nx.dot(x, w)
diff = Nx.subtract(y_pred, y)
gradient_descent =
x
|> Nx.transpose()
|> Nx.dot(diff)
|> Nx.multiply(1 / elem(x.shape, 0))
gradient_descent
|> Nx.multiply(alpha)
|> then(&Nx.subtract(w, &1))
end
defn mse(x, w, y) do
x
|> Nx.dot(w)
|> Nx.subtract(y)
|> Nx.pow(2)
|> Nx.sum()
|> Nx.divide(Nx.shape(x) |> elem(0))
end
end
Here are gradient_descent and mse functions. Notice that gradient_descent value gets multiplied by alpha, the learning rate. Basically, it determines how much weights are going to be changed. In other words, how git steps gradient descent is going to do in other to find the optimal solution.
Train the model!
The ML model is ready, so let's train it! In this approach, we're going to use only displacement as x.
model = %Model{
alpha: 0.1,
epochs: 200
}
trained_model = LinearRegression.train(model, x_std, y)
# Result
%Model{
weights: #Nx.Tensor<
f32[2][1]
EXLA.Backend<host:0, 0.3524400666.4193124372.233052>
[
[NaN],
[NaN]
]
>,
alpha: 0.01,
mse_history: [5914053.5, 86293921792.0, 1259188042858496.0, 1.8373901428369392e19,
2.681093018229369e23, 3.9122144076470293e27, 5.708641532863881e31, 8.329962648052612e35,
:infinity, :infinity, :infinity, :infinity, :infinity, :infinity, :infinity, :infinity,
:infinity, :nan,
...],
epochs: 200,
epoch: 200
}
Oops... It doesn't look promising. Something went wrong... Notice that MSE values went to infinity! It seems that alpha, the learning rate was too big. Let's give it another shot, with a smaller alpha.
model = %Model{
alpha: 0.0001,
epochs: 200
}
trained_model = LinearRegression.train(model, x, y)
# Result
%Model{
weights: #Nx.Tensor<
f32[2][1]
EXLA.Backend<host:0, 0.3524400666.4193124372.233454>
[
[0.09403946250677109],
[0.18162088096141815]
]
>,
alpha: 0.0001,
mse_history: [227.74842834472656, 209.40399169921875, 208.5283966064453, 208.4827117919922,
208.47647094726562, 208.4720916748047, 208.46778869628906, 208.46353149414062, 208.459228515625,
208.45492553710938, 208.45065307617188,
...],
epochs: 200,
epoch: 200
}
For alpha=0.0001 it calculated weights: b=0.09403946250677109 and w=0.18162088096141815 and got MSE ~208. Is it good? We won't know until we perform some tests!
3. Test the model
Coefficient of Determination (R2 )
To test the accuracy of our linear regression model we'll use the coefficient of determination, also known as R2. The formula looks quite simple.
$$R^2 = 1 - \frac{SS_{res}}{SS_{tot}}$$
Let's decipher the SS factors. The first one is the Sum of Squares of Residuals (also Residual Sum of Squares - RSS). It tells us about the distances of actual points to the prediction line. They're shown on the graph at the beginning of this post as red dashed lines (③).
The lower the SSres, the better.
$$SS_{res} = \sum_{i=1}^{n} (y'_i - y_i)^2$$
SStot is the Total Sum of Squares and it represents the distance between the actual values (labels) and the mean value line. In other words, the higher the SStot, the more variable labels are, making it more difficult to accurately predict the value.
$$SS_{tot} = \sum_{i=1}^{n} (y_i - \overline{y})^2$$
Can we calculate these factors using tensors? Yes! This time vectorized formulas are quite simple.
$$SS_{res} = \sum_{i=1}^{n} (Y' - Y)^2$$
$$SS_{tot} = \sum_{i=1}^{n} (Y - \overline{y})^2$$
The value of the coefficient of determination tells us how much the linear regression model is accurate. Now we'll analyze possible outcomes:
R2 = 1 - Ideal solution! 🦄 You probably won't see it in real life 😉
0 < R2 < 1 - Generally speaking, the closer to 1 the better, but anything above 0 is better than using the mean (y̅) for each guess
R2 = 0 - This is the same as using mean (y̅) for each guess. It's pretty much useless 🤷♂️
R2 < 0 - The model totally sucks and it's worse than using the mean for each guess! 🙉 The lower, the worse! And it may go down to oblivion...
It isn't fair, because we have literally the infinity (specifically negative infinity) of poor solutions and only 0-1 of somehow good ones. As one said: It is, what it is. 🤷♂️
Okay, now it's a good time for some code.
Calculating R2 in Elixir
The r2 function is pretty neat and readable. Nx supports all operations we need out of the box. 😉
defmodule LinearRegression do
defn r2(w, x, y) do
x = prepend_with_1s(x)
y_pred = Nx.dot(x, w)
# SS_res
res =
Nx.subtract(y, y_pred)
|> Nx.pow(2)
|> Nx.sum()
# SS_tot
tot =
Nx.subtract(y, Nx.mean(y))
|> Nx.pow(2)
|> Nx.sum()
# Coefficient of Determination
Nx.subtract(1, Nx.divide(res, tot))
end
end
Finally, let's test the trained model! We'll calculate r2 and MSE for the test set and will see how it went.
LinearRegression.test_mse(x_test, trained_model.weights, y_test)
|> Nx.to_number()
|> IO.inspect(label: "TEST MSE")
LinearRegression.r2(trained_model.weights, x_test, y_test)
|> Nx.to_number()
|> IO.inspect(label: "Accuracy")
# Result
TEST MSE: 236.6131134033203
Accuracy: -2.4155285358428955
r2 below 0 means, it's worthless! Why? Take a look at the MSE over epochs graph.
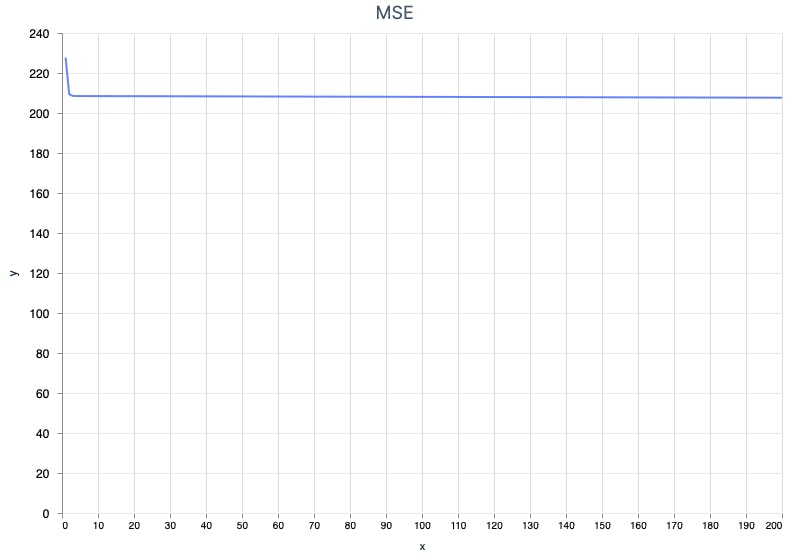
Okay, it seems it stopped learning pretty early.
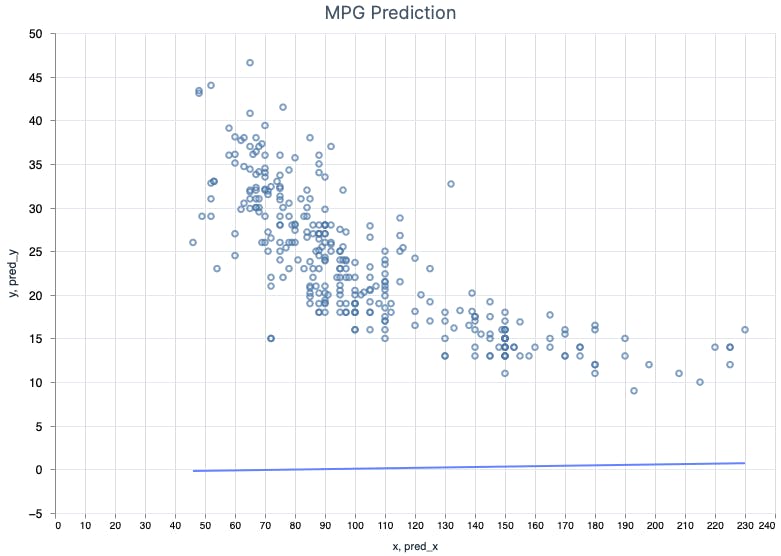
Dots are the data values, the line is our model. Shame. The prediction line is almost flat, close to 0. Is Python just better than Elixir in ML? 🙉
Why ML Model Doesn't Learn?
There are many possible reasons why the model doesn't perform training too well. The most common are:
Too few training examples - the more the better. In our case, we used ~320 examples, which is very poor
Improper features (
x) - some features are misleading, sometimes there are too many or too few. We used just one featuredisplacement. We can use more and we will.Features have "hard" values - when the features have weird, various values, it's much tougher for the model to find optimal weights. For instance,
displacementvalues land between 40 and 230,horsepower- 70-440,weight0.9-2.5.Improper learning rate - when it's too low, the model won't train fast enough, when it's too big, it'll overfit and go to infinity
We can't do anything about 1., but we can use more features and do something with values. The 4th point seems to be worth trying, but it's a topic for another post.
Test Model with standardized features
Adding more features seems to be a good idea, but they vary from each other, so the output probably will be even worse. That's why we'll try to make values more friendly for the ML model and put them on a similar scale first.
defmodule LinearRegression do
defn standardize_x(x, mean, std_dev) do
x
|> Nx.subtract(mean)
|> Nx.divide(std_dev)
end
end
x_mean = LinearRegression.x_mean(x)
x_std_dev = LinearRegression.x_std_dev(x)
x_std = LinearRegression.standardize_x(x, x_mean, x_std_dev)
x_test_std = LinearRegression.standardize_x(x_test, x_mean, x_std_dev)
In this case, we'll use standardization, known also as standard score or Z-score. Keep in mind that when you apply feature scaling for training, you need to scale test and prediction features as well! That's why you need to keep x_mean and x_std for making predictions.
Ready for tests with standardized features? Remember, we'll use just displacement but standardized. Okaay... let's go!
model = %Model{
alpha: 0.1,
epochs: 200
}
trained_model = LinearRegression.train(model, x_std, y)
LinearRegression.test_mse(x_test_std, trained_model.weights, y_test)
|> Nx.to_number()
|> IO.inspect(label: "TEST MSE")
LinearRegression.r2(trained_model.weights, x_test_std, y_test)
|> Nx.to_number()
|> IO.inspect(label: "Accuracy")
# Result
TEST MSE: 19.801504135131836
Accuracy: 0.6604369878768921
%Model{
weights: #Nx.Tensor<
f32[2][1]
EXLA.Backend<host:0, 0.3524400666.4193124372.238386>
[
[23.306041717529297],
[-6.024066925048828]
]
>,
...
}
Now we're talking! MSE is ~20, r2 ~0.66, which means that accuracy is about 66%. Not too shabby!
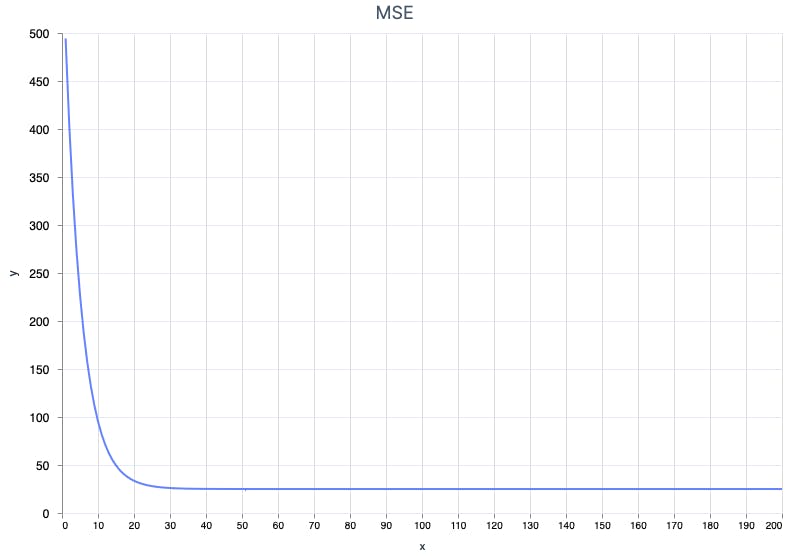
It looks like it found the optimal weights in just ~30 iterations. Nice!
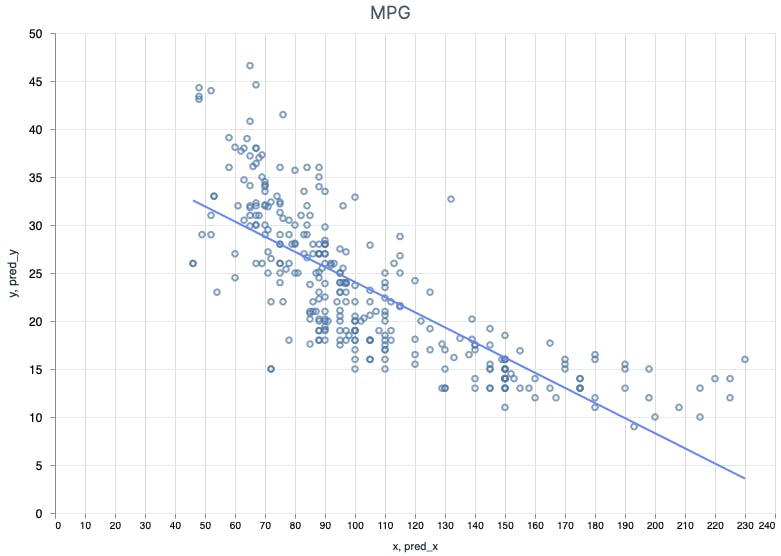
And here is the prediction line. Looks pretty good!
Test model with multiple features
One more test to go. This time we'll use displacement, horsepower and weight. My Gut tells me all of them are meaningful for the fuel consumption, let's check if it affects the model performance. We'll apply the standardization as in the previous point. Below x_test tensor before and after standardization.
# Before standardization
#Nx.Tensor<
f32[78][3]
EXLA.Backend<host:0, 0.3524400666.4193124372.233872>
[
[96.0, 122.0, 1.149999976158142],
[138.0, 351.0, 1.9774999618530273],
[170.0, 360.0, 2.3269999027252197],
...
]
>
# After standardization
#Nx.Tensor<
f32[78][3]
EXLA.Backend<host:0, 0.3524400666.4193124372.238814>
[
[-1.4333690404891968, -0.9660688042640686, -0.7269482612609863],
[-1.2810755968093872, -0.8996133208274841, -0.8212781548500061],
[-0.8495774865150452, -0.8996133208274841, -1.3208767175674438],
...
]
>
And here are the results of the final test.
TEST MSE: 18.814205169677734
Accuracy: 0.679672122001648
%Model{
weights: #Nx.Tensor<
f32[4][1]
EXLA.Backend<host:0, 0.3524400666.4193124372.240355>
[
[23.568984985351562],
[-1.7338991165161133],
[-1.9251408576965332],
[-3.1087865829467773]
]
>,
alpha: 0.1,
...
}
Accuracy is ~68%, just a little bit better. It's worth peeking at the graph showing predictions with respect to displacement.
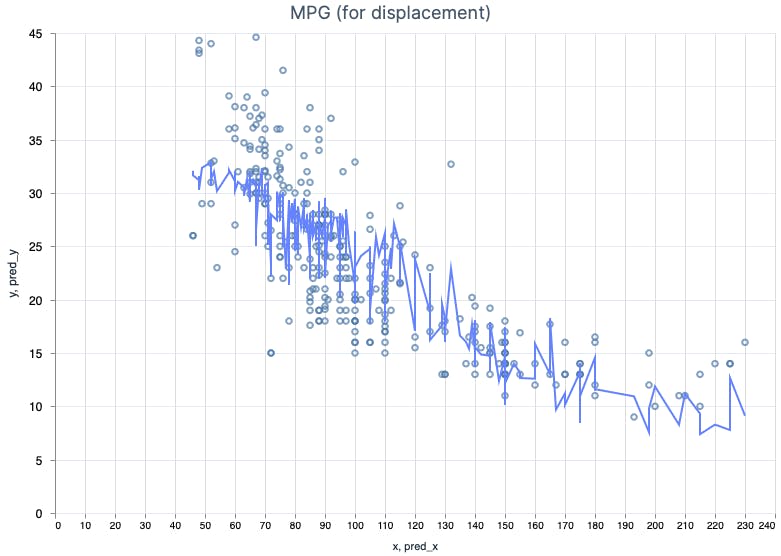
It isn't too straight, isn't it? 😉
4. Use The Model And Make Predictions!
We've already discussed everything except the most important part, at least from the end-user perspective - using the model to make predictions. Let's do it!
def predict(%Model{weights: w}, x) do
x
|> prepend_with_1s()
|> Nx.dot(w)
end
predict takes the trained mode, prepares the features, and multiplies them (matrix multiplication) by weights. Simple as that!
Friendly reminder: use mean and standard deviation calculated for training features and standardize the prediction features. In the other case, it won't work too well, delicately speaking...
x_std = LinearRegression.standardize_x(x, x_mean, x_std_dev)
y_pred = LinearRegression.predict(trained_model, x_std)
Nx.concatenate([y_pred, y], axis: 1)
# Result
#Nx.Tensor<
f32[392][2]
EXLA.Backend<host:0, 0.3093086062.301596692.234332>
[
[18.191600799560547, 18.0],
[15.069494247436523, 15.0],
[17.279438018798828, 18.0],
[17.566789627075195, 16.0],
[18.015308380126953, 17.0],
[9.754270553588867, 15.0],
[8.194624900817871, 14.0],
[8.847555160522461, 14.0],
[7.699560165405273, 14.0],
[12.580235481262207, 15.0],
[14.630147933959961, 15.0],
[15.787235260009766, 14.0],
[14.542545318603516, 15.0],
[12.289548873901367, 14.0],
[27.534603118896484, 24.0],
[24.272138595581055, 22.0],
[24.361839294433594, 18.0],
[25.539608001708984, 21.0],
...
]
>
Finally, we made use of the trained model and made predictions for the whole data set. As you can see in the result tensor, sometimes the model is almost perfect (see the first two value pairs), and other times is rather poor (9.75 vs 15). Anyway, it's not bad overall!
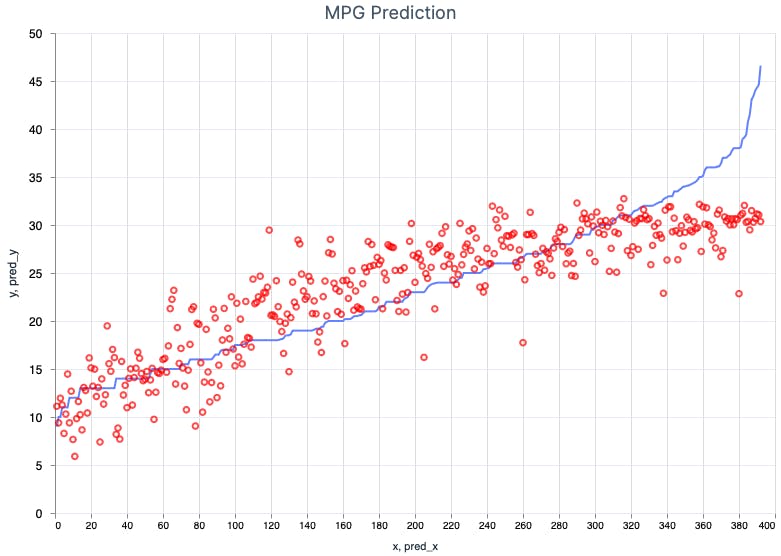
The graph above shows the actual MPG (y') as a blue line and predictions (y) as red dots. Before plotting the graph, I sorted it by y' to make it more readable. The model performs pretty well for smaller y' and worse for y' > 35.
Can it achieve better accuracy than 68%? I think so! It just needs some tuning, we'll do this in a future post. For now, it's time to wrap up
Linear Regression With Elixir - Conclusions
To be honest, this post is way more extensive than I planned, but I wanted to explain everything so it's clear for you and... future me 😉 Now I'll try to shorten everything in this bullet points list:
Linear Regression is pretty decent in predictions for some cases, especially when using multiple weights. In this case, it ended up with R2 of about 0.68 (in other words, an accuracy of 68%) which is nice!
Machine Learning is all about data, numbers, and math operations. That's why using dedicated libraries like Elixir Nx and operating on numbers using matrices is so important.
Features scaling as standardization helps you to get better results and get closer to the optimal solution much faster. If you decide to standardize the training features, remember to do the same for prediction features as well, that's why you need to store the mean and standard deviation determined for the training feature set.
The Gradient Descent technique is a bit tricky, but also widely used in the ML world. It's worth to learn it.
Optimizing the ML model is essential, especially when it's going to be used for big data
Determining the accuracy of the model is crucial, so it's important to find the right method of testing for the particular model. For linear regression, we used the coefficient of determination (R2)
The point of this post was to write the model from scratch and learn how things work on a low level
Bonus: Nx (& Elixir) did very well! 💜 Functions are quite intuitive to use. Writing code was fun and... much easier than describing everything in this post! 😅

