Table of contents
In the previous post, I described how to create a Linear Regression Machine Learning model in Elixir from scratch. This time we'll discuss so similar yet different beast - Logistic Regression.
Logistic Regression
First things first - what is this function, and what does it do? In short, Logistic Regression allows predicting the probability from 0 to 1 of occurring an event. Describing it more practically, it's used for solving classification problems.
For example, you can use logistic regression to determine how probable is that a recent email message you received is spam. In such a case, 0 would mean that the email is NOT spam, whereas 1 is definitely spam.
BTW, notice that the name Logistic "Regression" seems to be misleading, since it's often used as a binary classifier. The naming feels wrong...
Well, it returns any value between 0 and 1, so there are no finite classes of output. So in nature, it's a regression function. But often we pipe it to another function, checking, if the output is greater than 0.5. Then it's used as a classifier.
Linear Regression vs Logistic Regression
Logistic regression is related to linear regression. The biggest difference is the output values (y) are limited to 0-1 spectrum. You can easily notice the difference on the graph.
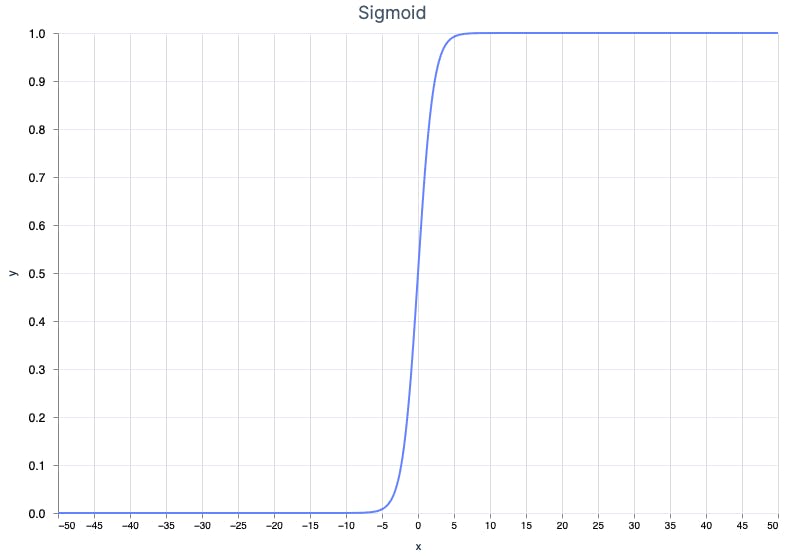
The center part of the graph resembles a steep linear function, but as it moves from the center toward the edges, the line becomes squeezed around 0 and 1. The function used by logistic regression is the sigmoid function, which is characterized by its distinct sigmoid curve shape.
Sigmoid Formula
The sigmoid function contains a linear function component in the denominator.
$$f(x) = \frac{1}{1+e^{-ax + b}}$$
When you think "in functions", it's the same old linear regression piped to the sigmoid function, which, as you would expect, is covered by the Nx library - Nx.sigmoid/1. So, we have a linear function, weights, and ready-to-go sigmoid function. It looks quite familiar. The difference is the output which can be anything between 0 and 1. In Machine Learning and statistics, we call it a logit.
Logit describes the probability, so it's kind of a scaled regression. Making a classifier out of it is pretty easy - after applying a sigmoid function, all you need to do is set some threshold like 0.5 and check if the value is greater than it (1 or "true") or lesser (0 or "false"). That's it!
Cost Function
In terms of the cost function, it turns out it's a totally different story than for linear regression. Recall that for linear regression Mean Squared Errors (MSE) method was the best option, which always converged to one, global minimum (Convex Function).
For logistic regression, MSE will have many local minima (it's non-convex), so it won't work. Fortunately, Binary Cross-entropy fits perfectly for classifiers as logistic regression. The formula of the loss function depends on the actual value, whether it's 1 or 0.
I used the following notation: y is a prediction, y' is an actual value and n is a number of examples.
$$\frac{1}{n} \sum\limits_{i=1}^{n} - log(y_i), \text{ if } y_i'= 1$$
$$\frac{1}{n} \sum\limits_{i=1}^{n} - log(1 - y_i), \text{ if } y_i'= 0$$
Calculating the cost function in two steps, for the actual value of 0 and 1 is not too exciting. The good news is that there's a simplified formula that handles both cases.
$$-\frac{1}{n} \sum\limits_{i=1}^{n} y'_i log(y_i) + (1 - y')log(1 - y_i)$$
As you might expect, there's a vectorized version of the equation that you can put easily to Nx, though you have to be careful when typing.
$$-\frac{1}{n}(Y'^T*log(Y) + (1-Y')^T log(1-Y))$$
Checking Logistic Regression Model accuracy
There's one more difference between linear and logistic regression which is checking the accuracy. Instead of Coefficient of Determination, for logistic regression, we use a super simple formula called Positive Rate. It checks how many predictions the model got right.
$$\frac{n_{correct}}{n}$$
Simple as that! In this case, the accuracy lies between 0 and 1. The closer to 1, the better. There's one issue with the metric though. It's not too useful for skewed data or when there are some special requirements on the "sensitivity" of the model. It's a bigger topic for another time, but just wanted to quickly mention here that another useful metric for classifiers is the Confusion matrix.
Alright, we covered already the theory, now is the time for Elixir and Nx in action!
Implementing Logistic Regression in Elixir
Linear regression and logistic regression have a lot in common, that's why I won't implement everything from scratch, but use the code from the article about Linear Regression with Elixir and make some adjustments so it works as a classifier.
Our job is to predict if the car from this dataset will pass emissions tests, based on all features... except the useless carname 😉. Let's take a look at the data.
| passedemissions | mpg | cylinders | displacement | horsepower | weight | acceleration | modelyear | carname |
| FALSE | 18 | 8 | 307 | 130 | 1.752 | 12 | 70 | chevrolet chevelle malibu |
| TRUE | 22 | 4 | 140 | 72 | 1.204 | 19 | 71 | chevrolet vega (sw) |
| FALSE | 18 | 6 | 225 | 105 | 1.8065 | 16.5 | 74 | plymouth satellite sebring |
Okay, so the data is the same as for linear regression but this time we'll use passedemissions as a label (y') and mpg as an additional feature.
Let's take a look at the changes in the code.
defmodule LogisticRegression do
alias NimbleCSV.RFC4180, as: CSV
import Nx.Defn
...
def load_data(data_path) do
data_path
|> File.stream!()
|> CSV.parse_stream()
|> Stream.map(fn row ->
[
passedemissions,
mpg,
cylinders,
displacement,
horsepower,
weight,
acceleration,
modelyear,
_carname
] = row
{[
parse_float(mpg),
parse_int(cylinders),
parse_int(horsepower),
parse_float(displacement),
parse_float(weight),
parse_float(acceleration),
parse_int(modelyear)
], [parse_boolean(passedemissions)]}
end)
|> Enum.to_list()
end
defn gradient_descent(x, w, y, alpha) do
y_pred = Nx.dot(x, w) |> Nx.sigmoid()
diff = Nx.subtract(y_pred, y)
gradient_descent =
x
|> Nx.transpose()
|> Nx.dot(diff)
|> Nx.multiply(1 / elem(x.shape, 0))
gradient_descent
|> Nx.multiply(alpha)
|> then(&Nx.subtract(w, &1))
end
defn cost(x, w, y) do
y_pred =
x
|> Nx.dot(w)
|> Nx.sigmoid()
term_one =
y
|> Nx.transpose()
|> Nx.dot(Nx.log(y_pred))
term_two =
y
|> Nx.multiply(-1)
|> Nx.add(1)
|> Nx.transpose()
|> Nx.dot(
y_pred
|> Nx.multiply(-1)
|> Nx.add(1)
|> Nx.log()
)
term_one
|> Nx.add(term_two)
|> Nx.divide(elem(y.shape, 0))
|> Nx.multiply(-1)
|> Nx.squeeze()
end
def predict(%Model{weights: w}, x) do
x
|> prepend_with_1s()
|> Nx.dot(w)
|> Nx.sigmoid()
|> Nx.greater(0.5)
end
defn accuracy(w, x, y) do
incorrect_count =
x
|> prepend_with_1s()
|> Nx.dot(w)
|> Nx.sigmoid()
|> Nx.greater(0.5)
|> Nx.subtract(y)
|> Nx.abs()
|> Nx.sum()
|> Nx.flatten()
y_count = elem(y.shape, 0)
y_count |> Nx.subtract(incorrect_count) |> Nx.divide(y_count)
end
end
First thing, notice each y_pred is piped to Nx.sigmoid() and next to Nx.greater(0.5) (except when calculating gradient descent). I split the crazy cost function so it's easier to digest. accuracy/3 function if completely different than for linear regression. There are also some cosmetic changes, like making names more generic (mse -> cost, r2 -> accuracy).
Test Logistic Regression model
model = %Model{
alpha: 0.2,
epochs: 200
}
trained_model = LogisticRegression.train(model, x_std, y)
LogisticRegression.test_cost(x_test_std, trained_model.weights, y_test)
|> Nx.to_number()
|> IO.inspect(label: "Test Cost")
LogisticRegression.accuracy(trained_model.weights, x_test_std, y_test)
|> Nx.to_number()
|> IO.inspect(label: "Accuracy")
# Result
Test Cost: 0.10394015908241272
Accuracy: 0.9743589758872986
Accuracy like ~0.97?! Considering this shallow learning with a dataset of just ~400 examples, it's pretty good!
Let's take a look at some graphs. First, cost over time or more precisely - epochs.
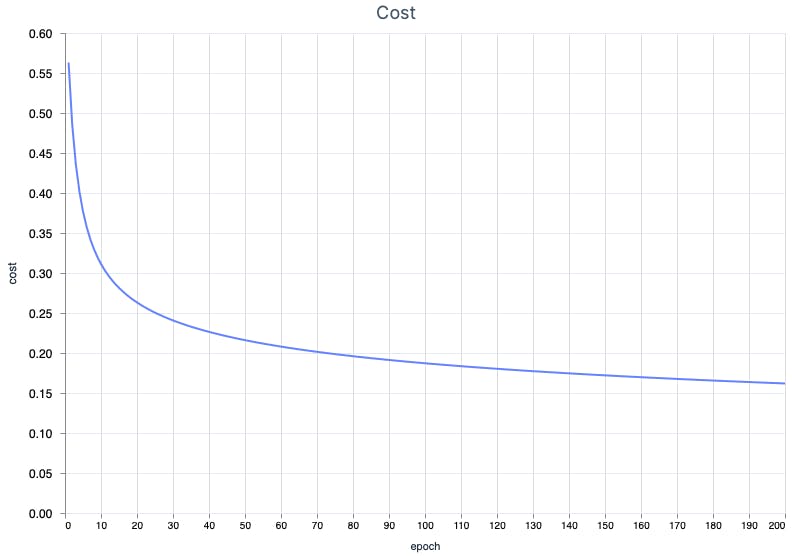
The initial cost is relatively low and goes down. It seems that cross-entropy works well for linear regression. Remember what I briefly mentioned about other metrics for classifiers, such as confusion matrix? Let's take a look.
| Predicted | Actual | Name | Count |
| 1 | 1 | True Positive ✅ | 53 |
| 1 | 0 | False Positive ❌ | 2 |
| 0 | 0 | True Negative ✅ | 23 |
| 0 | 1 | False Negative ❌ | 0 |
The model predicted correctly true 53 times and false 23 times. It went wrong two times, classifying false as true. Let's think about this for a minute. The model made 78 predictions on the test set, achieving a pretty good accuracy of ~97%. But, two cars made it through the emissions test (false positives), although they shouldn't...
Let's imagine that there are huge penalties for allowing cars to pass the emission test when they shouldn't (do you know the "Diselgate" scandal?). In such a case, an accuracy of 97% is not that impressive. We need to deal with false positives.
Tune Linear Regression with Precision and Recall
There are two more useful metrics for checking the performance of the classifier ML model - Precision and Recall. The two metrics are on the two ends of the spectrum, one end is marking "true" only when the model is very confident (higher precision, lower recall) and the other end is higher sensitivity (lower precision, higher recall).
Let's peek at the formulas, fortunately, they're quite clear.
$$precision = \frac{n_{true\_positives}}{n_{total\_predicted\_postives}}$$
$$recall = \frac{n_{true\_positives}}{n_{total\_actual\_postives}}$$
Both metrics take values from 0 to 1. So, in our case, precision = ~0.964 and recall = 1. But our business requirement is to have high precision. Can we change anything in the model to increase precision? Yes, we can and we'll do!
Let's peek at the predict function.
def predict(%Model{weights: w}, x) do
x
|> prepend_with_1s()
|> Nx.dot(w)
|> Nx.sigmoid()
# > logit e.g. 0.435, 0.975, etc.
|> Nx.greater(0.5) # <- threshold
# > classification, if greater than threshold then 1, 0 otherwise
end
Aha! We can easily adjust the threshold. 0.5 is quite a universal value and makes sense in many cases. But we'd like to increase precision - be more confident that true will really be true. So we need to increase the threshold. Let's give it a shot with value 0.8 and see what happens.
# Threshold 0.8
# Result
Training Cost: 0.14220784604549408
Test Cost: 0.2054743468761444
Accuracy: 0.8717948794364929
True Positive: 46
False Postive: 0
True Negative: 22
False Negative: 10
Precision: 1
Recall: 0.6764705882
Increasing the threshold from 0.5 to 0.8 caused the following effects:
The training cost didn't change - gradient descent uses a logit, so the threshold doesn't affect the training, just predicting
The test cost increased and accuracy dropped to ~0.87
There are no false positives and precision reached the perfect score
Recall went down from 1 to ~0.68 and there are 10 false negatives now
Even though the accuracy has decreased, the business goal has been achieved - the model does not approve any cars that should not pass the emission test 👍.
Confusion Matrix Heatmap
The confusion matrix can be shown as a heatmap. It's quite easy to generate with VegaLite lib.
# Confusion Matrix
alias VegaLite, as: Vl
Vl.new(title: "Confusion Matrix", width: 600, height: 600)
|> Vl.data_from_values(%{
predicted: Nx.to_flat_list(predictions),
actual: Nx.to_flat_list(actual)
})
|> Vl.mark(:rect)
|> Vl.encode_field(:x, "predicted")
|> Vl.encode_field(:y, "actual")
|> Vl.encode(:color, aggregate: :count)
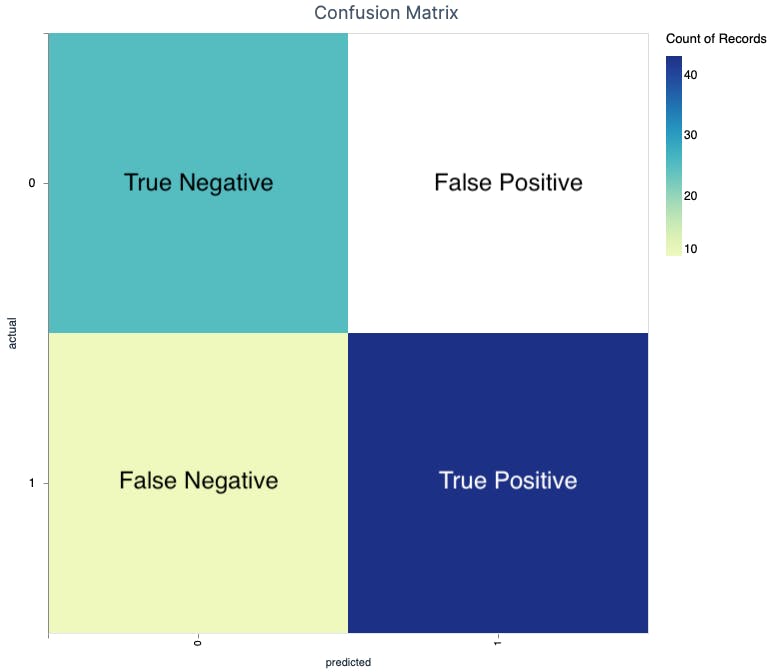
I added the labels, so everything should be crystal clear.
Conclusions
Implementing logistic regression based on the linear regression model wasn't too tough. The trickiest part was to write the cost function without any bugs - it's easy to make a mistake in the formula.
The logistic regression model we discussed did very well on the test data set, achieving an accuracy of 97%. After adjusting the threshold to increase precision and eliminate false positives, the accuracy dropped slightly to 87%. That's impressive, especially considering the small dataset of ~400 examples in total.
Linear/Logistic regressions are very important since they are the foundation blocks of neural networks. Won't be mistaken by naming them "shallow learning models". It doesn't sound fancy, but they're pretty powerful and much "cheaper" than deep learning methods.
| Linear Regression | Logistic Regression | |
| Type | Regression | Classifier (technically regression, when not classifying logit) |
| Output | -∞ – +∞ | 0 or 1 (technically 0 – 1, when not classifying logit) |
| Cost Function | Mean Squared Error | Binary Cross-entropy |
| Performance Metrics | R² Score | Positive Rate (also Confusion Matrix, Precision, Recall, F1 Score) |
| Achieved accuracy for the dataset | 68% (87% with feature engineering) | 97% |

