I already covered implementing Linear Regression model in Elixir from scratch. This time we'll move to implementing something fancy - Deep Learning model using a neural network under the hood! I'm going to use the same dataset so you'll have a nice 1:1 comparison.
MLP / ANN / Deep Learning
First things first - naming. It turns out it's a bit... problematic. The regression model I'm going to implement using a neural network could be named:
In terms of naming it's pretty much the same, and all of the names refer to neural networks with many layers of neutrons - that makes it "deep". Not sure why "deep learning" is so fancy and sounds better than "shallow learning"... But, hey! That's IT - everything is hype-driven! 😉 A few years ago we had a new BEST JS framework every week, now (2024) deep learning/AI and layoffs are trendy!
Okay, enough digressions. Let's briefly take a look at what the neural network looks like.
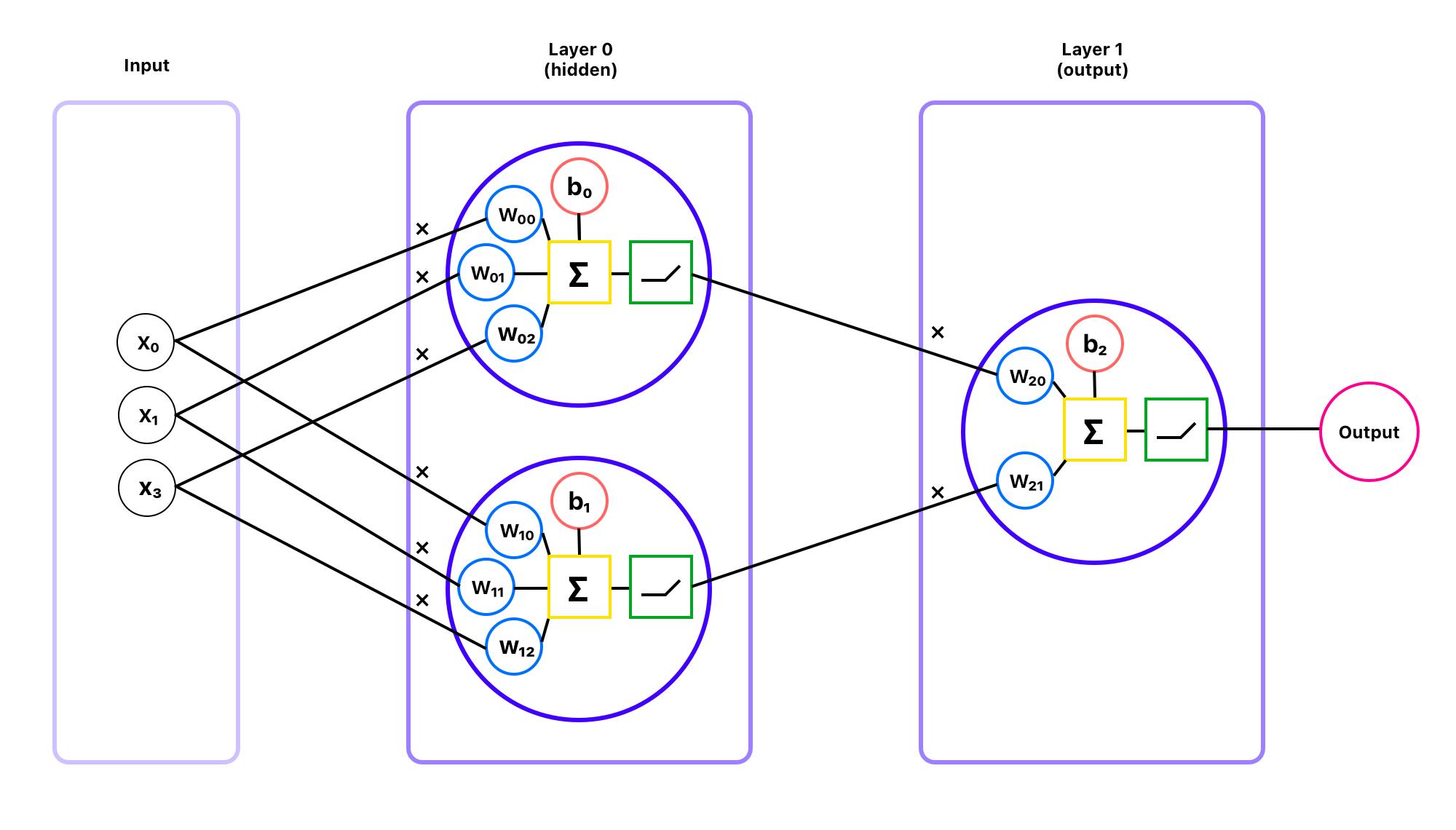
Usually, neural network graphs are simplified to circles and lines... but I wanted to show you the anatomy of a neuron, so I created my graph. So, starting from left: we have input with three features: x₀, x₁, and x₂.
All features are passed to neurons (purple circles) in Layer 0. The layers between input and output are called hidden layers because they're not "visible" to the user. Typically neural network is built of many hidden layers. Layer 0 contains two neurons.
Each neuron takes features and multiplies them by weights (blue circles), which are summed (yellow square) with a bias (red circle). Then, the result is passed to the activation function (green box). Output out of the neuron is passed to the next neuron, in this case, to the neuron in Layer 1.
Layer 1 in the example above is an output layer, since its output is the end result. The neuron in Layer 1 takes outputs from the neurons from Layer 0, multiplies them by weights, sums with bias, passes the result to the activation function, and... we have it!
Neurons in Neural Network
Each neuron has its own weights, bias, and activation function. Weights and bias are usually floats. The activation function is a math function. Its purpose is to introduce non-linearity, so the model can solve complex problems.
There are many activation functions in Nx library. The most common are relu, sigmoid, linear, and softmax. Linear and sigmoid sound familiar, don't they? What's interesting, if you apply linear as an activation function for all layers, you end up with... a linear function. It's a bad idea. Usually, the most commonly used activation function for hidden layers is relu (Rectified Linear Unit).
The choice of the activation functions is important, especially for the output layer. Here are my recommendations for some ML problems.
| ML Problem | Output Activation Function |
| Binary Classification | sigmoid |
| Multiclass Classification | softmax |
| Regression | linear |
How does Neural Network learn?
Neural Networks are supervised machine learning methods, which means they learn in the pretty much same way as linear or logistic regressions. During the training process, the model adjusts weights and biases for each neuron to minimize the cost function.
I think we discussed the theory and have a solid background to get our hands dirty and implement the MLP model using Axon.
Regression Neural Network with Axon
The plan is to create a regression neural network model predicting miles per gallon (MPG) for the given car features. It's exactly the same task as in Linear Regression with Elixir and Nx article. But this time instead of implementing everything from scratch, I'll use a dedicated library - Axon.
I'll reuse the data load processing function from the linear regression post. The dataset looks like this:
# {
# [passedemissions, cylinders, horsepower, displacement, weight, acceleration, modelyear],
# [mpg]
# }
[
{[0, 8, 130, 307.0, 1.752, 12.0, 70], [18.0]},
{[0, 8, 165, 350.0, 1.8465, 11.5, 70], [15.0]},
{[0, 8, 150, 318.0, 1.718, 11.0, 70], [18.0]},
{[0, 8, 150, 304.0, 1.7165, 12.0, 70], [16.0]},
{[0, 8, 140, 302.0, 1.7245, 10.5, 70], [17.0]},
{[0, 8, 198, 429.0, 2.1705, 10.0, 70], [15.0]},
...
]
We have a list of tuples consisting of features and labels. Let's split it to training and test sets. As before I use an 80-20 ratio.
{train_data, test_data} =
data
|> Enum.shuffle()
|> Enum.split(data |> length() |> Kernel.*(0.8) |> ceil())
So far, so familiar... Now, things get different. Axon's training function is Axon.Loop.run/4 which takes Enum or Stream split to batches as an argument. Due to the ML data nature and its size, using Streams is a much better idea. So, let's prepare the data.
batch_size = 4
train_stream =
train_data
|> Stream.chunk_every(batch_size, batch_size, :discard)
|> Stream.map(fn chunks ->
{x_chunk, y_chunk} = Enum.unzip(chunks)
{Nx.tensor(x_chunk), Nx.tensor(y_chunk)}
end)
test_stream =
test_data
|> Stream.chunk_every(batch_size, batch_size, :discard)
|> Stream.map(fn chunks ->
{x_chunk, y_chunk} = Enum.unzip(chunks)
{Nx.tensor(x_chunk), Nx.tensor(y_chunk)}
end)
batch_size determines the size of the examples batch. It's quite important to get this tuned, since increasing batch_size speeds up learning, but increases memory consumption and sometimes gives poor results. Small batches, on the other hand, converge better, giving smoother gradient descent, but are significantly slower. batch_size is one of the hyperparameters of the model, which means it's used for tuning and it's not being determined by the training itself.
Okay, it's a model creation time! Let's start with something "stupid" 😉 - just one neuron in the hidden layer and one in the output layer two neurons total
model =
Axon.input("car_features", shape: {nil, 7})
|> Axon.dense(1, activation: :relu) # hidden layer, just 1 neuron
|> Axon.dense(1) # output layer
# Result
#Axon<
inputs: %{"car_features" => {nil, 7}}
outputs: "dense_1"
nodes: 4
>
The model takes input with 7 features, passes them to the hidden layer with one neuron and the relu activation function then passes the result to the output layer with a linear activation function.
Axon provides nice functions for visualizing the model as a graph or table - let's try out the latter.
Axon.Display.as_table(model, Nx.template({1, 7}, :f32)) |> IO.puts()
# Result
+------------------------------------------------------------------------------------------------------+
| Model |
+===================================+=============+==============+=================+===================+
| Layer | Input Shape | Output Shape | Options | Parameters |
+===================================+=============+==============+=================+===================+
| car_features ( input ) | [] | {1, 7} | shape: {nil, 7} | |
| | | | optional: false | |
+-----------------------------------+-------------+--------------+-----------------+-------------------+
| dense_0 ( dense["car_features"] ) | [{1, 7}] | {1, 1} | | kernel: f32[7][1] |
| | | | | bias: f32[1] |
+-----------------------------------+-------------+--------------+-----------------+-------------------+
| relu_0 ( relu["dense_0"] ) | [{1, 1}] | {1, 1} | | |
+-----------------------------------+-------------+--------------+-----------------+-------------------+
| dense_1 ( dense["relu_0"] ) | [{1, 1}] | {1, 1} | | kernel: f32[1][1] |
| | | | | bias: f32[1] |
+-----------------------------------+-------------+--------------+-----------------+-------------------+
Total Parameters: 10
Total Parameters Memory: 40 bytes
Alright, so the model has 10 parameters total - 7 weights and 1 bias for the hidden layer. The output layers have 1 weight and 1 bias. The analogous linear regression model has 8 parameters - 7 weights and 1 bias, so it's pretty similar.
The model is ready to go, so now we're going to train it.
trained_model_state =
model
|> Axon.Loop.trainer(:mean_squared_error, :adam)
|> Axon.Loop.metric(:mean_absolute_error)
|> Axon.Loop.run(train_stream, %{}, epochs: 30)
# Console output
Epoch: 0, Batch: 150, loss: 785.9227295 mean_absolute_error: 22.4253941
Epoch: 1, Batch: 143, loss: 462.5274353 mean_absolute_error: 9.1923170
Epoch: 2, Batch: 136, loss: 336.9065247 mean_absolute_error: 7.2870026
...
Epoch: 29, Batch: 111, loss: 76.6344452 mean_absolute_error: 3.7401807
I used :mean_squared_error it as a loss function, :adam as a gradient descent optimizer, :mean_absolute_error (MAE) as a cost indicator and set the model to train through 30 epochs.
As you noticed in the result, MAE decreased from ~ 22 to ~4, which looks promising.
Testing the model
Training is done. Now it's time for testing. Let's start with checking the MAE for the test data set.
model
|> Axon.Loop.evaluator()
|> Axon.Loop.metric(:mean_absolute_error)
|> Axon.Loop.run(test_stream, trained_model_state)
# Result
Batch: 77, mean_absolute_error: 3.8084450
MAE for the test is similar to the result for training, which means that probably the model doesn't overfit.
Anyway, we need some more meaningful metrics like the R2 score, the same as we used for the linear regression model. This time I'll use the r2_score/3 function from the Scholar library.
{x_test, y_test} =
test_data
|> Enum.unzip()
|> then(fn {x, y} ->
{Nx.tensor(x), Nx.tensor(y)}
end)
{_, predict_fn} = Axon.build(model)
y_pred =
predict_fn.(trained_model_state, x_test)
Scholar.Metrics.Regression.r2_score(Nx.flatten(y_test), Nx.flatten(y_pred))
|> Nx.to_number()
|> IO.inspect(label: "Accuracy")
# Result
Accuracy: 0.5886043906211853
To make predictions you need to build the prediction function and use the trained model. It looks a bit odd at first, but you can get used to it.
R2 of ~0.59 is not bad, but not spectacular either. Let me remind you that linear regression with feature standardization resulted in an R2 of about 0.68, with some feature engineering it reached R2 = ~0.87. So, something is off...
How to improve the MLP regression model?
As usual, I have a few tricks that we can use to quickly improve our regression model.
Increase neurons/layers number - our model has only 2 neurons! In terms of capability, it's more stupid than a roundworm - a "little-primitive-disgusting bug" (sorry biologists!) that proudly carries 302 neurons 😮! Generally speaking, increasing the complexity of a neural network, increases its capability. Capability is not equal to performance. And the more complex the model gets, the more expensive it is. So as always - it's a tradeoff.
Fix underfitting/overfitting - Simply speaking underfitting usually means you have too little/bad training data. Overfitting occurs when the model does noticeably worse in tests than in training. I guess that's our case.
Tune hyperparameters - try changing some parameters like number of epochs, batch size, change optimizer, etc.
Adjust architecture - there are many types of neural network architectures working better for some kinds of problems, like CNN, RNN, etc. To be honest, I'm not aware of anything specific for regression.
Okay, let's introduce some tweaks and give it a shot!
batch_size = 1
# ...
model =
Axon.input("car_features", shape: {nil, 7})
|> Axon.dense(32, activation: :relu)
|> Axon.dense(8, activation: :relu)
|> Axon.dense(1)
trained_model_state =
model
|> Axon.Loop.trainer(:mean_squared_error, :adam)
|> Axon.Loop.metric(:mean_absolute_error)
|> Axon.Loop.run(train_stream, %{}, epochs: 40)
# ...
# Result
Batch: 77, mean_absolute_error: 2.3542204
Accuracy: 0.8551386594772339
Decreasing the batch size (4 → 1) and increasing the number of neurons (2 -> 41) and epochs (30 → 40) improved the R2 score from ~0.59 to ~0.86. MAE decreased from ~3.8 to ~2.4.
That's impressive for just 41 neurons. I bet the mentioned roundworm (remember, 302 neurons according to scientists) couldn't do this better! 😛
Let's take a look at how changing the two-neuron layer to two layers with 32 and 8 neurons changes the architecture of the model.
+-------------------------------------------------------------------------------------------------------+
| Model |
+===================================+=============+==============+=================+====================+
| Layer | Input Shape | Output Shape | Options | Parameters |
+===================================+=============+==============+=================+====================+
| car_features ( input ) | [] | {1, 7} | shape: {nil, 7} | |
| | | | optional: false | |
+-----------------------------------+-------------+--------------+-----------------+--------------------+
| dense_0 ( dense["car_features"] ) | [{1, 7}] | {1, 32} | | kernel: f32[7][32] |
| | | | | bias: f32[32] |
+-----------------------------------+-------------+--------------+-----------------+--------------------+
| relu_0 ( relu["dense_0"] ) | [{1, 32}] | {1, 32} | | |
+-----------------------------------+-------------+--------------+-----------------+--------------------+
| dense_1 ( dense["relu_0"] ) | [{1, 32}] | {1, 8} | | kernel: f32[32][8] |
| | | | | bias: f32[8] |
+-----------------------------------+-------------+--------------+-----------------+--------------------+
| relu_1 ( relu["dense_1"] ) | [{1, 8}] | {1, 8} | | |
+-----------------------------------+-------------+--------------+-----------------+--------------------+
| dense_2 ( dense["relu_1"] ) | [{1, 8}] | {1, 1} | | kernel: f32[8][1] |
| | | | | bias: f32[1] |
+-----------------------------------+-------------+--------------+-----------------+--------------------+
Total Parameters: 529
Total Parameters Memory: 2116 bytes
Total number of parameters increased from 10 to 529. This means more computations, time, and memory are required for the training.
Linear Regression vs Neural Network Regression
In the end, the linear regression model with feature engineering, performed almost the same as the neural network model after tuning, achieving an accuracy of about 85%. Although the results look pretty much the same, there are totally different kinds of beasts.
Take a look at this oversimplified, yet still instructive table.
| Liner Regression | Neural Network | |
| ML Problems | Just regressions | Regressions, binary/multi-classifications |
| Input/output relationship | Just linear (+ simple non-linear with feature engineering) / "simpler" | Linear and highly nonlinear / "complex" |
| Data preparation | Very important | Just helpful |
| Training time | Fast | Slow |
| Resources consumption | Cheap | Expensive |
| Finding input/output correlations | Easy | Impossible |
| Achieved accuracy (R2) | 68% (87% with feature engineering) | 85% |
| Hype | 😐 | 🙂 (🤩 - when deep learning) |
It's hard to compare linear regression to neural networks, since the latter may solve different kinds of problems, so I'll focus just on the regression. In terms of choice between them, IMO the most important is the relationship between input and output. In other words, the linearity of the data.
When you deal with a complex problem when the features match with labels in some crazy pattern, basically you have no choice - neural network is the only viable choice. ANN has amazing capabilities - it can deal with super complex data without special preparation. It's kinda a silver bullet. BUT...
Neural Networks are greedy. Training and running predictions with ANN are much more expensive in both resources and time. That's where linear regression shines.
Linear regression is a great choice for linear or simple input/output relationships. It requires more work with feature engineering the data, but once it's set - it trains and works super fast.
Oh no, I forgot about the hype... Forget linear regression, there's no such a thing. Go with neur... Deep Learning! 🚀
Deep Learning in Elixir - Conclusions
Again, the Elixir ecosystem proves it can handle machine learning, like neural networks without any problem. Axon does the job well! TBH I don't have too much experience with ML in Python using PyTorch or TensorFlow, but Nx + Axon duet looks very solid and IMO it's a viable option. Especially you can transfer Elixir ML models from/to Python using ONNX (Open Neural Network Exchange) tools like AxonOnnx.
Elixir is still a bit exotic, I know. It's a big shame that it hasn't gotten the hype it deserves. But I've gotten used to that. Anyway, I'm very grateful to all the contributors for such a great ecosystem 🙏. And there's LiveView Native on the horizon... Can't wait! 💜

